How do we know what we know in science?
What is the distance from the Earth to the moon? You can easily find that information using a smart phone and Google. Google says that distance is 238,900 miles.
 Fine, but how do you know that value is right? Google’s business is not astronomical research. No doubt Google got the value from some “Scientific Authority.” Do you believe Google? Do you believe Scientific Authority? How do you know the moon isn’t just on some dome up there, way above the clouds? Seriously—how do you know? You may simply believe Authority, but plenty of people do not. Just recently Neil deGrasse Tyson felt the need to respond to rapper B.o.B’s assertion that the world is flat, an idea no more absurd than the moon being on a dome above the clouds.
Fine, but how do you know that value is right? Google’s business is not astronomical research. No doubt Google got the value from some “Scientific Authority.” Do you believe Google? Do you believe Scientific Authority? How do you know the moon isn’t just on some dome up there, way above the clouds? Seriously—how do you know? You may simply believe Authority, but plenty of people do not. Just recently Neil deGrasse Tyson felt the need to respond to rapper B.o.B’s assertion that the world is flat, an idea no more absurd than the moon being on a dome above the clouds.
So how might people like B.o.B, who question Scientific Authority, verify the moon’s distance for themselves? After all, science is not supposed to be about accepting things on Authority. Science is supposed to be about testing, replicating, and verifying the results of others. And yes, it is in fact possible to verify the distance to the moon.
Imagine that you live in Grand Forks, ND, and you have a friend who lives a great distance due south of you, in Victoria, TX. You both have small telescopes and decent cameras. You both agree that at 10:00 PM tonight you will photograph the moon. But first, you each have to calibrate how many degrees the field of field of view of your camera-plus-telescope covers, so you can use it to make measurements of things in the sky.
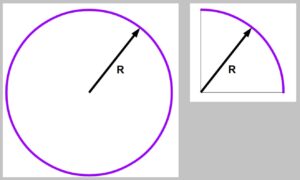
How do you do this? You take a photo of a 1-foot ruler at a set distance away. Remember that the circumference C of a circle whose radius is R is given by the formula C=2πR. The length of a sector S of a circle marked out by some angle is a fraction of the circumference: S=(Angle/360o)C. For example, if the angle is 90 degrees, then you have a quarter circle and the sector length S is S=(90o/360o)C. That is (1/4)C, or 1/4 the circumference of a circle of radius R.
You want to determine what a degree is in your camera-plus-telescope. So, at what distance will the ruler need to be so that it measures 1 degree as seen in any pictures you take with your camera-plus-telescope? Using S=1 foot and Angle=1 degree, you go to your formulas:
S=(Angle/360o)C
1 ft=(1o/360o)C
C=360 ft
Next, to find the distance (which will be R):
C=2πR
360 ft=2πR
360 ft/2π=R=57.3 ft
Therefore if you set up the ruler 57.3 ft away and take a photo of it through your telescope, the length of the ruler will be 1 degree.
With the calibration complete, you and your friend proceed to take pictures of the moon tonight, with the results being as shown below. Note the difference between these two photos! The moon is not in the same place relative to the stars when seen from Grand Forks as when simultaneously seen from Victoria. Why not?
 Simulated moon photographs taken from Grand Forks, ND (left) and Victoria, TX (right). Simulation made using the Stellarium planetarium software.
Simulated moon photographs taken from Grand Forks, ND (left) and Victoria, TX (right). Simulation made using the Stellarium planetarium software.The answer is parallax. As shown in the figure below, observers at two different locations A and B on Earth will see celestial objects in different positions against the stars. And this is very cool. Why? Because parallax means we can do triangulation—we can use angles to measure distances.
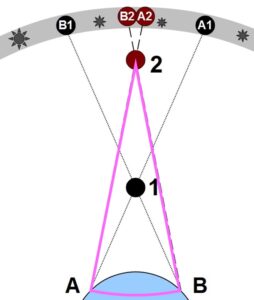
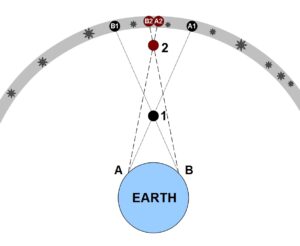 Object 1 appears among the stars at A1 as seen by an observer on Earth at A, but it appears at B1 as seen by an observer at B. The difference between the two positions is the parallax of the object. Object 2 is more distant from Earth and thus has a lesser parallax—there is a lesser difference in the positions of Object 2 as seen by the two observers.
Object 1 appears among the stars at A1 as seen by an observer on Earth at A, but it appears at B1 as seen by an observer at B. The difference between the two positions is the parallax of the object. Object 2 is more distant from Earth and thus has a lesser parallax—there is a lesser difference in the positions of Object 2 as seen by the two observers.Let’s superimpose a sector of a circle on our parallax diagram, as seen below. We make point A be Victoria, point B be Grand Forks, and Object 2 be the moon. Now, the sector angle between A and B is the same as the angle between the different moon positions on the sky, A2 and B2, as seen from Victoria and Grand Forks.
Using your calibration ruler and the photo software on your computer, you measure the moon to have a diameter of 0.92” on your photos. This turns out to be half the length that your calibration ruler measures in photos, so 0.92” translates into the diameter of the moon being 0.5 degrees. This 0.5 degree value happens to agree with what you have read from The Scientific Authorities! So far, so good.
Now you use the photo software to overlay the two pictures. To measure the angle between the two moon positions, you find a small, distinct feature on the moon (arrowed in green below) and use it to measure the difference in the moon’s position. You find it moved 0.07” horizontally, and 0.52” vertically. Since the Pythagorean Theorem says a2+b2=c2, you can calculate the total distance it moved: 0.52469”. At 1 degree for 0.92”, that translates into 0.28516 degrees.
 Measuring the difference in the moon’s position using a distinct feature on the lunar surface—a small dark spot.
Measuring the difference in the moon’s position using a distinct feature on the lunar surface—a small dark spot.The next thing you need is the distance from A to B—the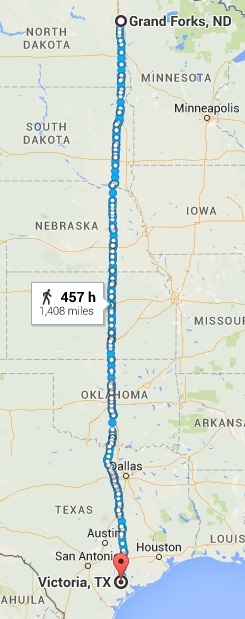 distance from Grand Forks to Victoria. You refuse to accept anything on Authority, so you decide to bicycle from Grand Forks to Victoria. You outfit the bike with a precision odometer you personally calibrated to ensure that it measures distance correctly. You follow the most direct route, even taking walking paths if need be. You discount the mileage of any side trips. And, after a month-long cycling trip, your odometer tells you that the distance from Grand Forks to Victoria is 1408 miles.
distance from Grand Forks to Victoria. You refuse to accept anything on Authority, so you decide to bicycle from Grand Forks to Victoria. You outfit the bike with a precision odometer you personally calibrated to ensure that it measures distance correctly. You follow the most direct route, even taking walking paths if need be. You discount the mileage of any side trips. And, after a month-long cycling trip, your odometer tells you that the distance from Grand Forks to Victoria is 1408 miles.
Now you know the distance from A to B on the sector is S=1408 miles, and the sector angle is 0.28516 degrees. Back to the equations to determine the sector’s radius R, which is the distance from Object 2 (the moon) to A or B:
S=(Angle/360o)C=(Angle/360o)2πR
1408 miles=(0.28516o/360o)2πR
R=(360o/0.28516o)(1408 miles/2π)=282,900 miles
Ta-da! You and your friend have just calculated the distance to the moon. 282,900 miles is not the same as Google’s 238,900, but it is definitely “in the ball park.” And, you made a lot of approximations in your work. You ignored the differences between the distances measured from A to B across the curved surface of the Earth vs. along the sector of the circle centered on the moon. Your picture overlay and picture distance measurements were crude. Your route was not direct—every turn and jog would lengthen the A-B distance (and likewise make your calculated R too large). The moon was high in the sky when you took the pictures, but not directly overhead like in the parallax diagram. There was much room for improvement in your work. Yet nonetheless your value for the moon’s distance generally agrees with Google’s—to within 20%! And you measured that distance entirely on your own. You relied on no Authority. You used only a phone camera, a small telescope, a ruler, and a bicycle. And you used one other very important thing: you used reason to determine the distance to the moon.
Triangulation is an old method of measuring distances. Note that the two key measurements involved in it are the distance between A and B, and the angle. These measurements can be made without any modern technology. In the 16th century, before even the telescope had been invented, Tycho Brahe made angle measurements to accuracies of better than 1/30 the diameter of the moon by means of instruments that were essentially giant protractors. Brahe could have told you the distance to the moon through triangulation.
 Left—Tycho Brahe. Right—An illustration of Tycho’s astronomical instruments, all of which are angle-measuring devices of one sort or another.
Left—Tycho Brahe. Right—An illustration of Tycho’s astronomical instruments, all of which are angle-measuring devices of one sort or another.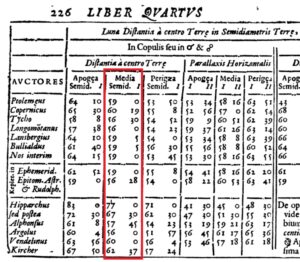 A table from Giovanni Battista Riccioli’s 1651 Almagestum Novum giving parallax and distance information for the moon, according to various astronomers dating all the way back to Hipparchus in antiquity (Tycho Brahe included). Average distances range from 56 to 77 times the radius of Earth, or 224,000 to 308,000 miles. The result discussed here fits right into this range.
A table from Giovanni Battista Riccioli’s 1651 Almagestum Novum giving parallax and distance information for the moon, according to various astronomers dating all the way back to Hipparchus in antiquity (Tycho Brahe included). Average distances range from 56 to 77 times the radius of Earth, or 224,000 to 308,000 miles. The result discussed here fits right into this range.Note also that, at least in principle, the distance to any object in the heavens might be measured this way. In fact, triangulation is the only direct method of measuring distances to most things in space. The problem is that the farther the object in question, the smaller the angle (as seen with Object 1 and Object 2 in the parallax diagram), and if the angle is too small it will be impossible to measure. Brahe actually tried to measure the distance to Mars this way in an effort to test whether Copernicus was right in his ideas about the universe, but could not get good enough measurements.
This is how we know stuff in astronomy. We know through reason—through observations, measurements, and calculations. It makes sense. You can try it for yourself. Enjoy the ride!